- Overview
- Objective
- Assumptions
- Theoritical Efficient Quantity of Staked QI
- Simulated Scenarios
- Simulation Flow
- Results
- 2. Exchange Rate 1550, 40M Benqi staked AVAX
- 3. Exchange Rate 1000, 40m Benqi staked AVAX
- Edge Cases Drill Down
- 3. Minimum Risk Premium is 50% and Price Impact is 0%
- 4. Minimum Risk Premium is 50% and Price Impact is 1%
- Conclusions
- About Chaos Labs
Overview
Popular on blockchains that utilize Proof of Stake consensus protocols, Liquid Staking refers to an innovative approach to staking in which a user can stake their tokens without losing access to them. The tokens have been staked (often by delegating this process to a third party), but they’re still available as liquidity, hence the name ‘Liquid Staking’.
As Liquid Staking becomes a more mature and important approach to securing blockchains, it becomes necessary to quantify, analyze, and answer certain questions. In particular, we want to know whether veQI is beneficial for both validators and BENQI tokenholders and, if so, what is the optimal model and parameterization for achieving the maximum utilization veQI?
To address these questions we must first understand the potential validator's motivations. What are the primary incentives for validators, and what is the upper bound on the upside they can capture? What are the economic risks and deterring factors for potential validators which must be weighed against this upside? When is Qi staking profitable enough for validators to be incentivized to participate? Can we predict veQI staking strategies and how it impacts the efficiency of Liquid Staking as a whole?
Getting clarity on these complex technical matters is our purpose in this document.
Objective
Benqi’s goal is to create a Liquid Staking model that is beneficial to validators while aligning their incentives to that of the QI community.
The simplified QI staking plan is to delegate the 30% of staked AVAX to validators according to their proportional holdings of veQi (proportional holdings are also referred to as their ‘weight’). veQi is emitted along similar lines as the PTP - vePTP model and veQI validators are able to set delegation fees from 2% to 5%.
1 staked PTP generates 0.014 vePTP every hour. The maximum vePTP held from a deposit is 100 times the PTP staked. In other words, it takes about 10 months to reach the vePTP cap. You can always stake more PTP to earn more vePTP, and you can withdraw your staked PTP at any time, but your accumulated vePTP will drop to 0 as soon as you unstake any amount.
For our analysis, the anchoring data we used was:
- AVAX validators make ~8% APR from their staked AVAX
- The circulating supply of QI is 2.9B
- The price of 1AVAX = 1680QI
- The total amount of sAVAX in Benqi is approximately 5M
Assumptions
Our model makes the following assumptions:
- All validators are rational.
- There is an unlimited supply of Qi at the current price.
- Validators consider the risk of holding QI equal to the risk of holding AVAX.
- Qi will not be un-staked if the validator continues validating, and we assume all of them do. Under this assumption, over a period of time greater than a year $veQi(user) ~= stakedQi(user)$
Theoritical Efficient Quantity of Staked QI
What follows from these robust assumptions?
First, the maximum extractable value to the protocol from staked QI is 5% of overall AVAX rewards. The value of the AVAX staked by validators can therefore be expressed
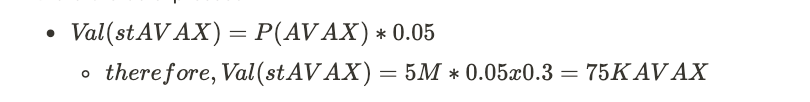
From this (and assumption #3 above) it follows that the total value of QI which grants the right to receive 1.5M AVAX in delegations will be 75K AVAX (around $1.425M at current price levels).
Based on assumption #2, there is an unlimited supply of QI at the current price, so
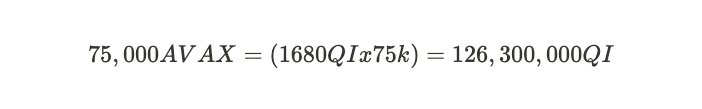
If all validators are rational (assumption #1), we should expect that approximately 123,300,000QI will be purchased and staked. Given that the circulating supply of QI is about 2.69B, the percent locked QI will be:
Simulated Scenarios
In a real-world scenario, we assume validator behavior will tend to converge to rational behavior because the competition amongst a large number of actors will tend to drive out market inefficiencies.
We have simulated different scenarios which test various levels of risk appetite and price impact. Each scenario was tested over 10 delegation epochs, and in each epoch, we simulated a group of validators assessing the profitability of buying QI based on two varying parameters:
- their risk appetite, i.e. the risk premium they require in order to hold QI over AVAX
- the price impact of buying QI.
Defining Risk Appetite
The risk appetite of validators is measured by their willingness to buy QI instead of holding AVAX, which would grant them an equivalent value in rewards. On the whole, we anticipate risk appetite among validators will increase over time as they grow to trust QI and as they see the first validators acquiring (and staking) QI.
We simulated a range of risk appetite scenarios by translating it into a price discount they require in order to hold QI instead of AVAX. In each simulation, the initial price discount validators expect in order to hold QI over AVAX is 90%. As expected, over the course of the simulation risk the price discount decreases to the range of 0%-50%, indicating growth in risk appetite.
Price Impact
Price Impact is hard to predict as there are other stakeholders already holding QI. We measure this by simulating a range of price impact scenarios. For Every 1M QI bought by validators, we estimate a price increase by D, ranging between 0% and 1%
Simulation Flow
We approached simulation by computing potential validators (using either real or synthesized validator data), as follows.
- For each epoch in [0,T-1], grant existing users new $veQI, with one staked QI generating $e$ units of $veQI every round.
- Delegate available $AVAX to users according to their weight (i.e. their share of $veQI), up to their max capacity. Delegations only last a single epoch, so terminate any made 1 epoch prior to the current round.
- Then, estimate new staking in the current epoch.
1. Staking QI is only profitable if :
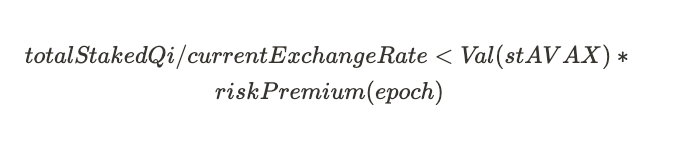
- If this condition holds, calculate the amount of QI required to buy staked AVAX delegation,
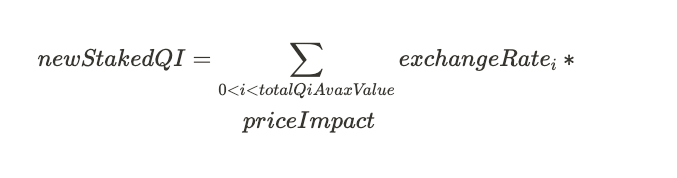
Then, randomly select a set of validators such as their total capacity < staked AVAX, and have them buy and stake a new QI amount. With that done calculate the new exchange rate the new risk premium.
Results
We executed 100 simulations for every set of parameters, randomizing the validator staking order for each simulation. Relevant validator data (eligibility, capacities, etc.) is based on a snapshot of current data from the network (taken on 09/19/22). Each simulation is run for 20 epochs, where each epoch is 14 days. The risk premium is increased every epoch and the QI market price increases for every 1M QI bought.
Below is the mean result for each simulation configuration:
1. Current Market Conditions (9/19/22) - Exchange Rate 1680, Total Benqi staked AVAX is 5M
Each point in the map represents the total amount of Qi staked in simulation under a given configuration of price impact and risk premium. Assuming 0% price impact (assumption #2) and 100% risk appetite (assumption #3), we get an upper bound of 116M on the amount of staked Qi (bottom left corner), which accords with the upper bound calculated above.
Intuitively, we would expect the upper bound to be reduced linearly by introducing a risk premium (Y axis). A higher price impact reduces the amount of staked QI tokens, but the value of staked QI in terms of AVAX should remain the same along the X axis.
Total Staked QI[M]
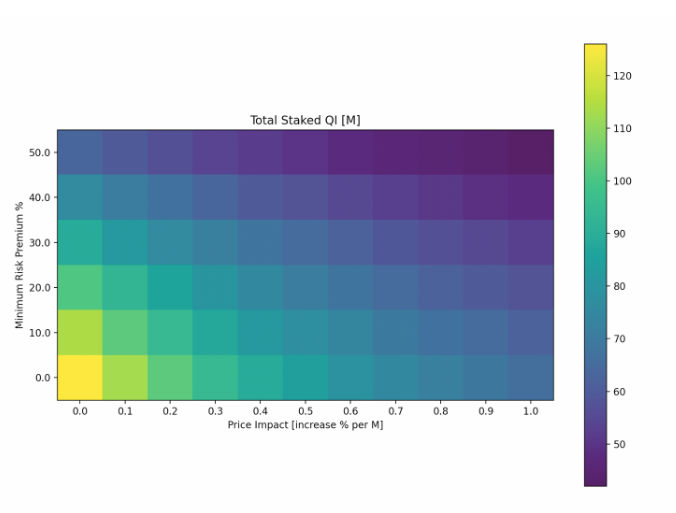
Each point in the map represents the total amount of Qi staked in simulation under a configuration of price impact and risk premium. Assuming 0% price impact (assumption #2) and 100% Risk appetite (assumption #3), we get the upper bound on the amount of staked Qi of 123M (bottom left corner), equating to the bound calculated above. Intuitively, we would expect the upper bound to be reduced linearly by introducing a risk premium (Y axis). A higher price impact reduces the amount of staked QI tokens, however value of staked QI in terms of AVAX should remain the same along the X axis.
Final AVAX: QI Exchange Rate
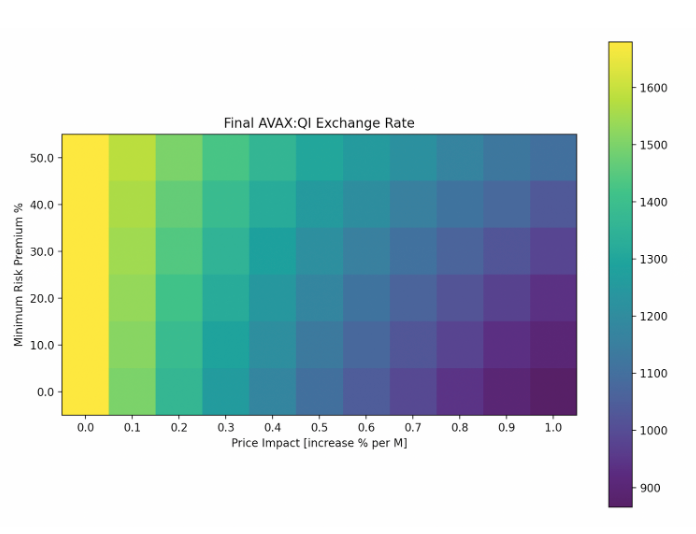
We see the significance of price impact on the amount of QI that can be locked. It gets less profitable to stake additional QI as the token price increases. However, that is a desired outcome of the protocol, as it creates a high dependency between AVAX and QI prices.
2. Exchange Rate 1550, 40M Benqi staked AVAX
We ran a separate scenario with increased AVAX staked in Benqi, representing approximately 15% of AVAX circulating supply.
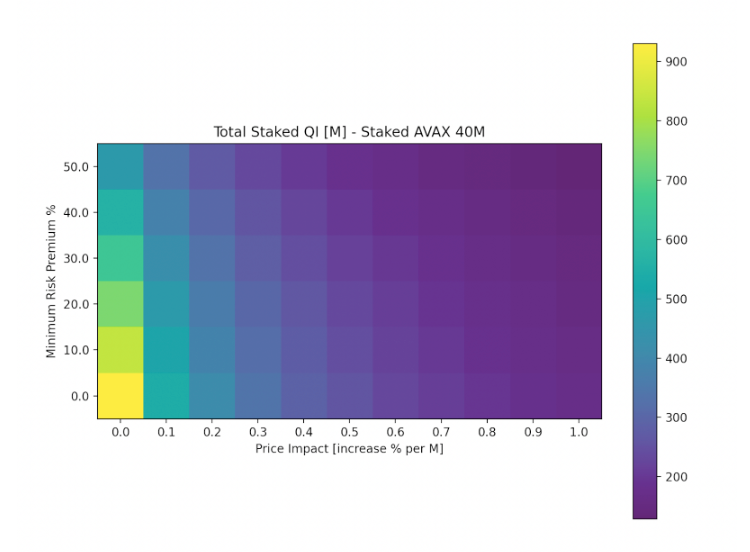
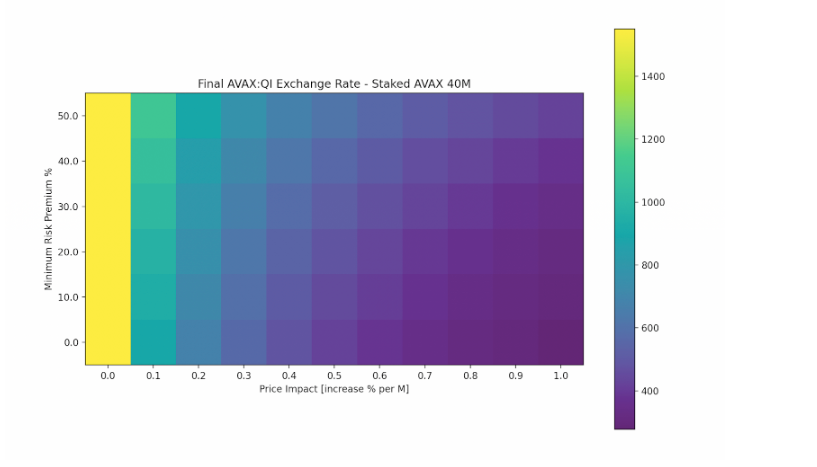
3. Exchange Rate 1000, 40m Benqi staked AVAX
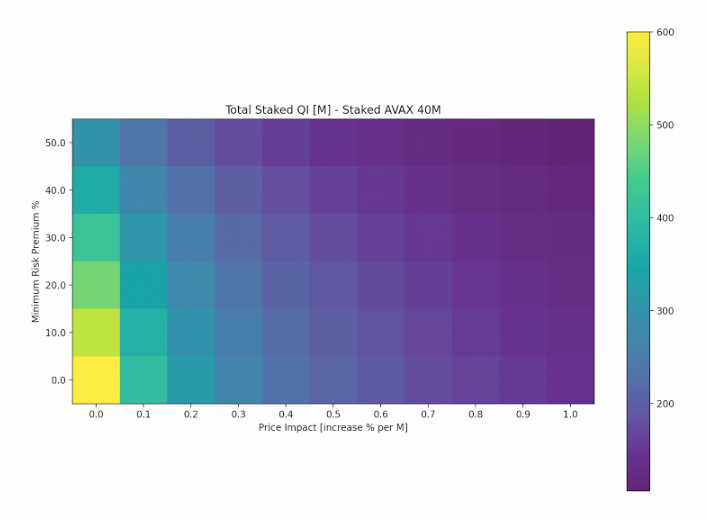
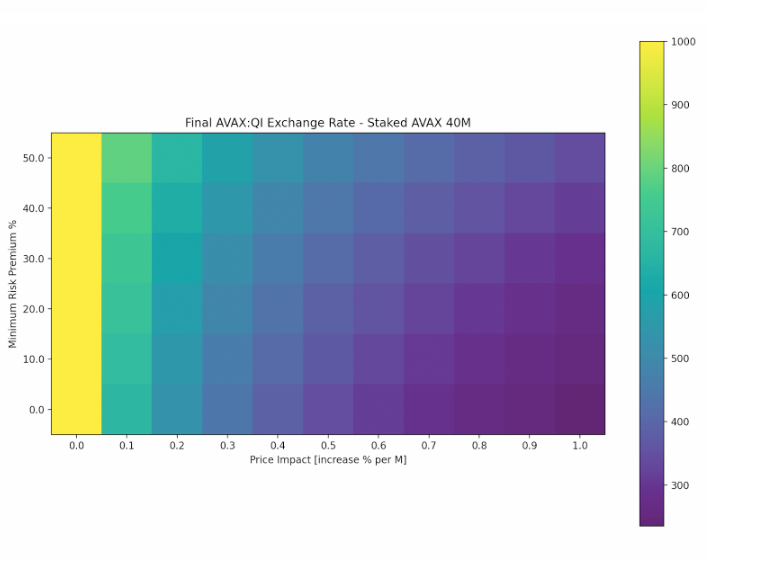
Edge Cases Drill Down
1. Minimum Risk Premium is 0% and Price Impact is 0
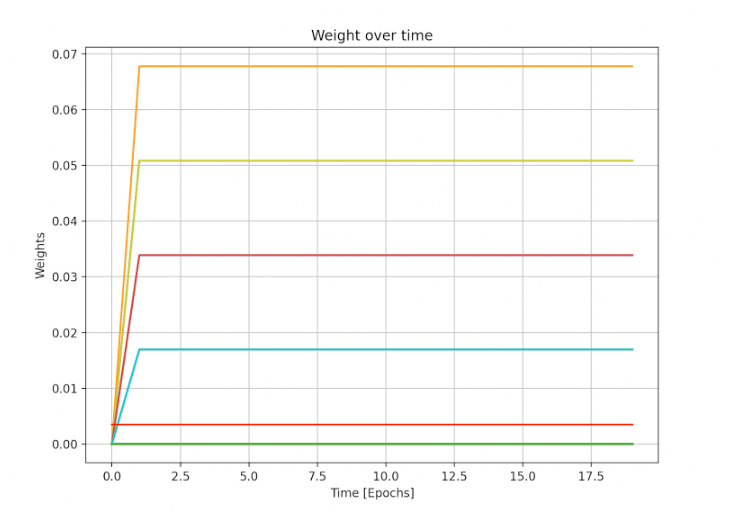
In the best-case scenario (bottom left corner of heat map), a total of 116M $QI were staked by validators, at a total cost of 75K AVAX. Below are the results per each validator:
Each plot in the figure below represents a single validator. As risk premium decreases rapidly, we see the entire amount of QI staked in the first 2 epochs. Over 20 epochs we see the weights stabilize as veQI(user) ~= stakedQi(user), which shows the validity of assumption #4.
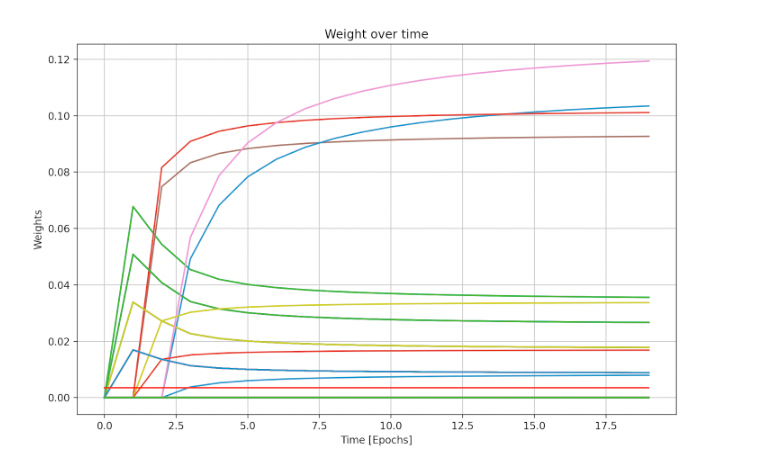
Weights of validators (veQI relative amount owned by validator) over the course of the simulation.
2. Minimum Risk Premium is 0% and Price Impact is 1%
n this scenario we introduce the effect of 1% price impact (bottom right corner of heat map) - for every 1M QI bought, the AVAX-QI exchange rate decreased by 1%. a total of 63M $QI were staked by validators, at a total cost of 75K AVAX. Below are the results per each validator:
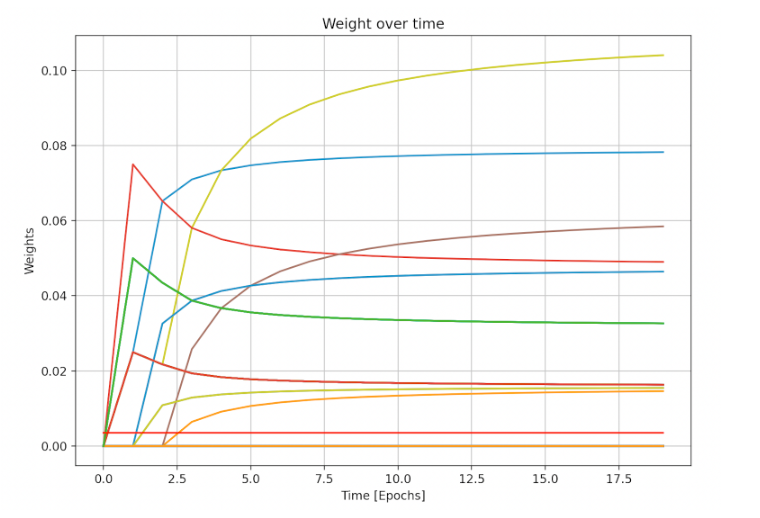
Weights of validators (veQI relative amount owned by validator) over the course of the simulation.
The weight distribution remains similar, as risk appetite grows at the same rate as scenario 1, and assumption #4 still holds. We can see the QI
exchange rate goes down to ~830 after ~60M Qi is bought.
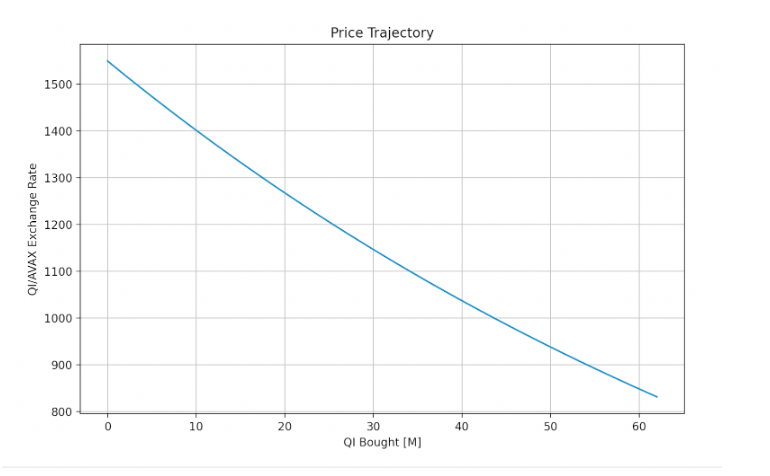
Price Trajectory - Amount of 1 AVAX: QI, change over amount of QI bought for staking.
3. Minimum Risk Premium is 50% and Price Impact is 0%
In this scenario, we assume validators would demand a minimum of 50% risk premium over the entire course of the simulation (upper left corner of the heat map). This effectively reduces the price a given validator would be willing to pay for Benqi-staked AVAX by 50%. A total of 59M $QI were staked by validators, at a total cost of 38K AVAX. Below are the results per each validator:
4. Minimum Risk Premium is 50% and Price Impact is 1%
In terms of total QI locked (the upper right corner of the heat map), this scenario represents the worst case. The combined effect of the high minimum risk premium and the high price impact lead to a total of only 40M $QI staked by validators, at a total cost of 30K AVAX. Below are the results per each validator:
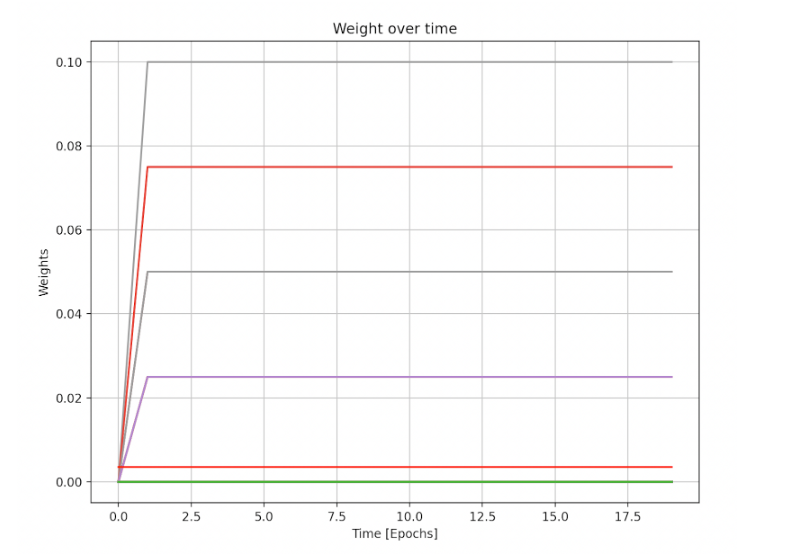
Weights of validators (veQI relative amount owned by validator) over the course of the simulation.
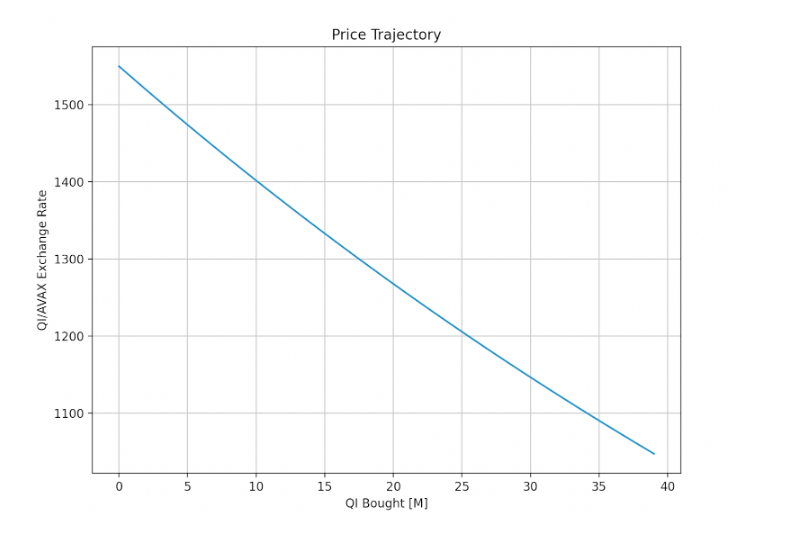
Price Trajectory - Amount of QI: 1 AVAX, change over amount of QI bought for staking.
Conclusions
These simulations can tell us many things about the incentives and market dynamics of this ecosystem. First, we see that increasing staked AVAX in BENQI should linearly increase the amount of QI staked as veQI in the protocol. Second, a high-risk premium actually increases validators’ profit, as validators receive the same amount of delegation but are willing to pay less for it. Third, we expect the actions of rational market participants to eventually drive the minimum risk premium demand to 0%--but bear in mind the difficulty of predicting the rate of risk appetite growth and the different risk profiles of validators if assumption #1 doesn’t hold. And finally, as long as assumption #4 holds price impact reduces the amount of Qi tokens locked, but does not affect the value locked in terms of AVAX.
Validators who are early to stake can realize outsized ROI compared to those who stake later, due to the yield of accumulated rewards. We are building an associated BENQI Liquid Staking ROI Calculator to better measure this opportunity (similar to the Rewards Calculator built for dYdX).
If you are an AVAX validator and want to learn more, please contact us at benqi@chaoslabs.xyz.
About Chaos Labs
Chaos Labs is a software company building a simulation platform to allow teams to efficiently test protocols and understand how they will react to adversarial market environments. The backbone of our technology is a cloud-based, agent- and scenario-based simulation platform that allows users to orchestrate blockchain state, test new features, and optimize risk parameter selection.
Our technology allows users to:
- Orchestrate protocol/blockchain state
- Generate wallets with behavioral attributes
- Test protocol performance in chaotic market conditions
- Optimize risk parameters
Our mission is to secure and optimize protocols through verifiable agent- and scenario-based simulations.
The Chaos Labs simulation platform is built to emulate a production environment. Each simulation runs on a mainnet fork with the chain's current state so that your simulations include up-to-date account balances and the latest contracts and code deployed across DeFi. You cannot look at your protocol in a silo when you're testing adversarial environments. You must ensure you understand how external factors such as cascading liquidations, oracle failures, variable gas fees, liquidity crises, and more will impact your protocol in various situations.
